清宮俊雄著「幾何学-発見的研究法-」(科学新興新社, ISBN4-89428-188-0)の 35ページに次の定理が載っています (記号と表現は少し変えてあります)。
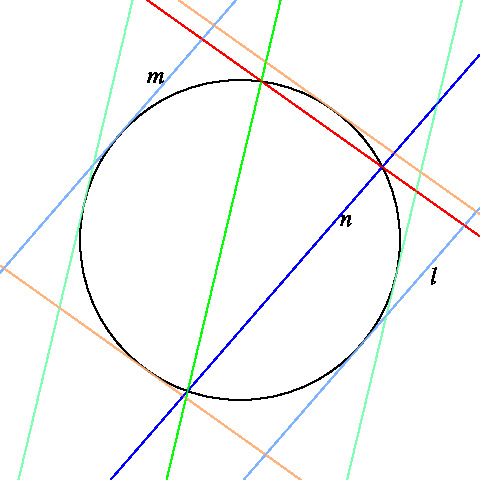
「三角形 ABC と直線 l があるとき,
頂点 A, B, C から l への垂線の足からそれぞれ BC, CA, AB への垂線は一点で交わる。」

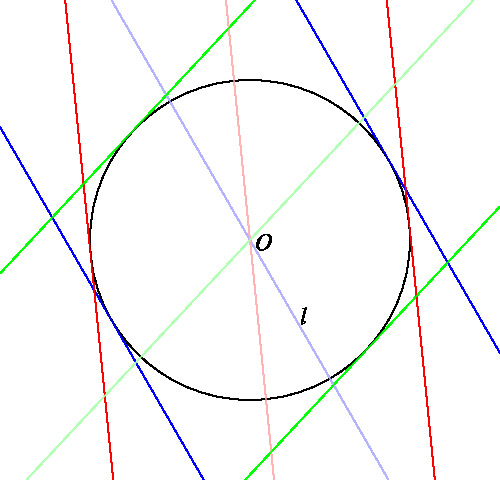
左図の A, B, C, G と l はマウス
(タブレットならば指)で動かせます。

PCならば 左の画面内でダブルクリック,
タブレットならば A, B, C, G, l
から離れた所で画面にタッチすれば
以下の説明にある C(G) (黄色の曲線)と
⊿ABC の外心, 外接円(灰色),
デルトイド曲線(薄緑色)を表示します。

　上の定理の直線 l に対して結論の交点を P(l) とし, 点 G に対して C(G) = { P(l) | l は G を通る直線} とします。
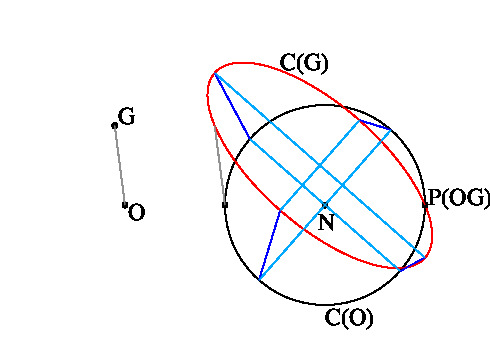
　定理 1　⊿ABC の外接円の半径を r, 点 G と ⊿ABC の外心との距離を d とするとき, C(G) は長軸, 短軸の長さがそれぞれ d + r, |d - r| の楕円である。 特に, G が ⊿ABC の外心ならば, C(G) は ⊿ABC の九点円であり, G が ⊿ABC の外接円上にあれば, C(G) は長さが 2r の線分である。

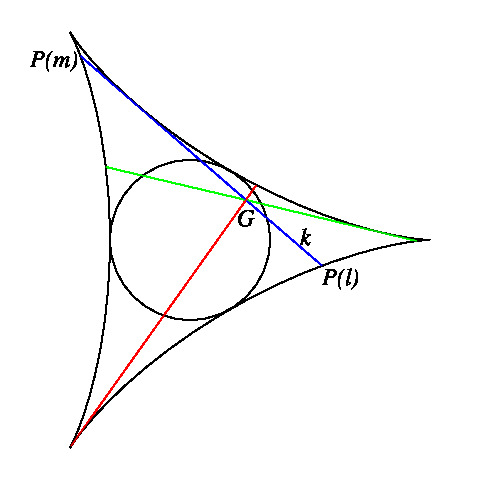
　点 P に対して P(l) = P となる直線 l の本数を n(P) とします。
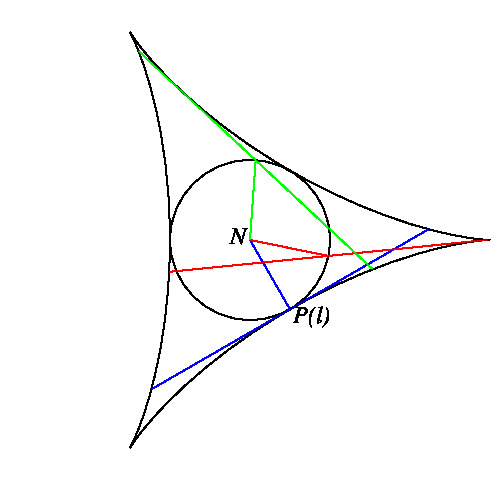
　定理 2　⊿ABC の三辺と⊿ABC の九点円に三点で接するデルトイド曲線が存在し (左下図参照), P がその曲線の内部にあれば, n(P) = 3 であり, 尖点を除く曲線上にあれば, n(P) = 2 である。 また, P がその曲線の尖点であるか曲線の外部にあれば, n(P) = 1 である。 　　　　　 　　　　　 　上の定理のデルトイド曲線の内部の点 P に対して P(l) = P となる三本の直線 l を辺とする三角形を Δ(P) とします。
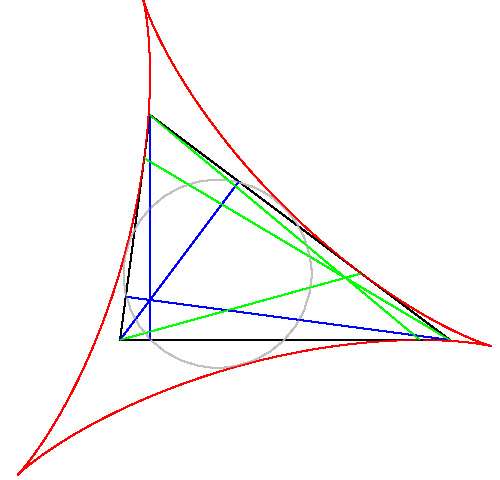
　定理 3　Δ(P) は ⊿ABC の外接円に内接し(上中央図参照), 次の (a),(b),(c) が成り立つ。
　(a) Δ(P) は正三角形 ⇔ P は⊿ABC の九点円の中心　(右上図参照)
　(b) Δ(P) は二等辺三角形 ⇔ P は上のデルトイド曲線と九点円の接点と反対側のデルトイド曲線の尖点を結ぶ直線上の点
　(c) Δ(P) は直角三角形 ⇔ P は九点円上の点

　定理 1 の証明の概略　P(l) に関して次が成り立ちます。
　(1) l が辺 BC に直交していれば, P(l) は l と BC の交点である。
　(2) l が頂点 A を通れば, P(l) は A から BC への垂線上にある。 さらに, l が⊿ABC の外心も通れば, P(l) は A から BC への垂線の足である(証明)。
　(3) l が直線 BC ならば, P(l) は⊿ABC の垂心である。
　(4) l が直線 BC に平行ならば, P(l) は垂心を l と BC の距離だけ l に直交する方向に移動したものである。 さらに, l が ⊿ABC の外心を通れば, P(l) は A と⊿ABC の垂心を結ぶ線分の中点である。
　以下で示すように C(G) は線分または楕円になりますので, G が⊿ABC の外心ならば, 上の (1), (2), (4) より, C(G) は⊿ABC の九点円になります。 また, G が⊿ABC の外接円上にあるならば, (1) より, C(G) は G に対する⊿ABC のシムソン線に含まれる線分になります。
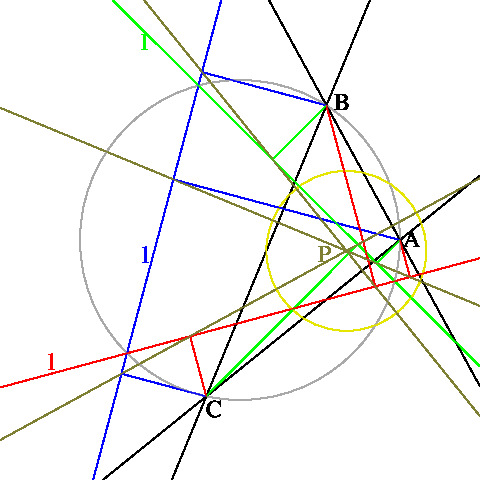
　A から G を通る直線 l への垂線の足 H は GA を直径とする円の上にあります。 この円の中心を O とするとき, ∠AOH = 2∠AGH ですから, l と x軸のなす角を s とすれば, 定数 a_x, a_y, a_c,, a_d, α により, H から BC への垂線は a_xx + a_yy = a_c + a_dcos(2s - α) で表されます((a_x, a_y) は BC の方向ベクトル)。 同様に, B から l への垂線の足から CA への垂線は b_xx + b_yy = b_c + b_dcos(2s - β) で表されます。 この 2 直線の交点の軌跡即ち C(G) は α - β が π の整数倍のときは線分, それ以外のときは楕円になります。
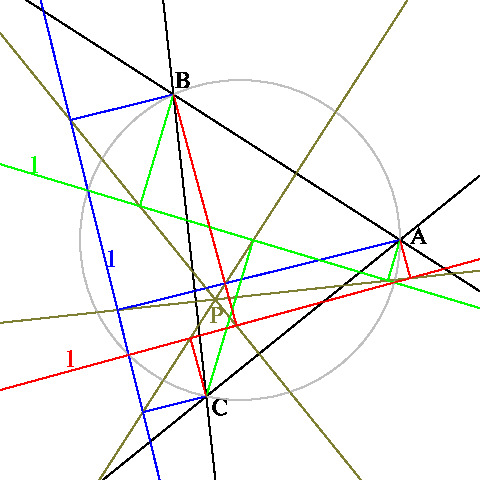
　O を⊿ABC の外心とし, N を⊿ABC の九点円の中心とします。 O を通る直線 l が半回転するとき, P(l) は N の周りを一回転します。 このとき, l の回転方向と NP(l) の回転方向は逆であり, l と NP(l) が平行となる l は三本であることが次のようにしてわかります。

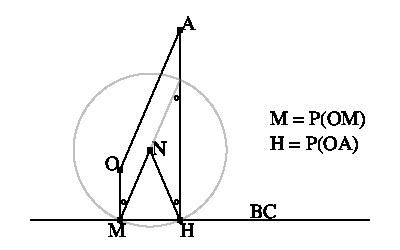
　l の回転方向と NP(l) の回転方向が同じかまたは逆であるかに応じて, l と NP(l) が平行となる l は一本または三本です。 辺 BC の中点を M とし, A から BC への垂線の足を H とします。 M = H ならば, A は OM 上にありますから (2) より, OM と NP(OM) は同じ直線です。 M と H が異なれば, OA と MN は平行ですから, OA と NH のなす角は OM と NM のなす角の二倍です(左上図参照)。 また, H = P(OA) であり, H を通って OA に平行な直線を HN に重ねる回転方向と MO を MN に重ねる回転方向は逆です。 したがって, Q を九点円 C(O) の弧 MH 上の点で ∠HNQ = 2∠QNM となる点とし, l を O を通って NQ に平行な直線とすれば, P(l) = Q となります。 辺 CA, AB に対しても同様ですから, O を通る直線 l で l と NP(l) が平行となるものが三本あります。
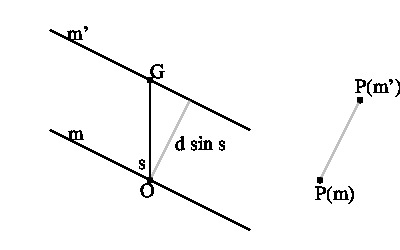
　m と m' が平行な直線のときは, P(m) の定義から明らかに P(m') は P(m) を m に直交する方向へ m と m' の距離だけ移動したものになります。 したがって, m, m' がそれぞれ O, G を通り, m と OG のなす角が s のとき, 線分 OG の長さを d とすれば, P(m') は m に関して G と同じ側で, m に直交する方向に P(m) を d sin s だけ移動した点になります (上中図参照)。 このことから, 少し面倒な計算をすると 半直線 NP(OG) から半直線 OG への回転角を t とするとき, C(G) の短軸, 長軸の方向と NP(OG) のなす角はそれぞれ t / 2, (t + π) / 2 であり, ⊿ABC の外接円の半径(=九点円の直径)を r とすれば, 長軸, 短軸の長さはそれぞれ d + r, |d - r| となることがわかります(上右図参照)。

　定理 2 の証明の概略　直線 l に対して l^{^} = { P(m) | m は l に平行な直線} は P(l) を通って l に直交する直線です。 n(P) は外心 O を通る直線 l で l^{^} が P を通るものの本数です。 l が O の周りを半回転する間に l^{^} も同じ方向に半回転し, P(l) は九点円 C(O) 上を反対向きに一回転ますので l^{^} は C(O) に外接するデルトイド曲線の接線であることがわかります。 NP(l) と l が平行となるとき l^{^} は C(O) に接しますから, このデルトイド曲線も P(l) で C(O) に接します(下図参照)。
　 (1) より, 辺 BC は上記のデルトイド曲線の接線です。 BC とデルトイド曲線の接点を D とし, BC の中点を M, A から BC への垂線の足を H とすれば, デルトイド曲線の接線の性質より, D, M, H はこの順に等間隔です(下図参照)。 n(P) はこのデルトイド曲線の接線で P を通るものの本数ですから, n(P) = 2 となる点 P の軌跡はこのデルトイド曲線から３つの尖点を除いたものです。 また, P がこの曲線の内部の点ならば n(P) = 3 であり, P が外部の点または尖点ならば n(P) = 1 です。 　定理 3 の証明の概略　l を O を通る直線で NP(l) と平行になるものとします。 このとき, P(l) は上のデルトイド曲線上の点です。 m を O を通る直線とし, Q = P(m) とします。 上で見たように NP(l) と NQ のなす角は l と m のそれの二倍で l を m に重ねる回転方向と NP(l) を NQ に重ねるそれは逆です。 m' を m に平行な ⊿ABCの外接円の接線とすれば, QP(m') は m に直交し, 長さが ⊿ABCの外接円の半径( = C(O) の直径) の線分です(下図参照)。 デルトイド曲線の性質より P(m') は上のデルトイド曲線上の点です。 また, m を O を通り l に直行する直線とすれば, P(m) は P(l)P(m) が C(O) の直径となる点です。 m' を半直線 NP(l) の方向に C(O) の半径だけ m を平行移動した直線とすれば, P(m') ＝N となります。 　　 　G を ⊿ABCの外接円上にない点とします。 上で見たように G を通る相異なる二直線 l と m に対して P(l) と P(m) は楕円 C(G) 上の相異なる点です。 G が ⊿ABCの外接円上の点のときは線分 C(G) の端点でない点 Q に対して P(l) = Q となる直線 l は丁度二本です。 したがって, P(l) = P(m) を満たす相異なる二直線 l と m の交点(平行ならば, P(l) と P(m) は l と m の距離だけ離れた点となります) は ⊿ABCの外接円上の点であり, P(l) = P(m) = P(n) を満たす相異なる三直線 l, m, n に対してそれらの交点 lm, mn, nl は ⊿ABCの外接円上の相異なる点です。
　(a), (b), (c) は上記を参考に少し考えればわかります。 また, デルトイド曲線内の点 G に対して G からデルトイド曲線への接線がわかれば, Δ(G) もわかります(下図参照)。 k を G からデルトイド曲線への接線とし, l を k に直交する ⊿ABCの外接円の接線とすれば, P(l) は k とデルトイド曲線の交点の一つです。 l を G と P(l) の距離だけ平行移動した直線を n とすれば, P(n) = G です。