デルトイド曲線 　デルトイド曲線とは大きい円の内側を半径が三分の一の円が転がるときその円の上に固定された点の描く軌跡です。 大きい円の中心が原点で半径が 3 であり, 転がる円上に固定された点が最初に (3, 0) にあれば, デルトイド曲線は x = f(t), y = g(t) で表されます。 ここで f(t) = 2cos t + cos2t,　　g(t) = 2sin t - sin 2t です。 この曲線の P = (f(t₀), g(t₀)) での接線 l は (sin t₀/2)x + (cos t₀/2)y = sin 3t₀ /2 で表されますが, これは Q = (cos t₀, sin t₀) を通って, 方向ベクトルが (cos t₀/2, -sin t₀/2) の直線です。
　また, 大きい円と中心が同じで半径が三分の一の円を C とすれば, 転がる円は Q で C に接しています。 転がる円と C は同じ半径ですから, l と C の交点で Q と異なる方を R とすれば, Q を中心に 180度回転したとき, P は R に重なります。 したがって, P, Q, R はこの順に等間隔です(下図参照, デルトイド曲線は青線, l は赤線)。 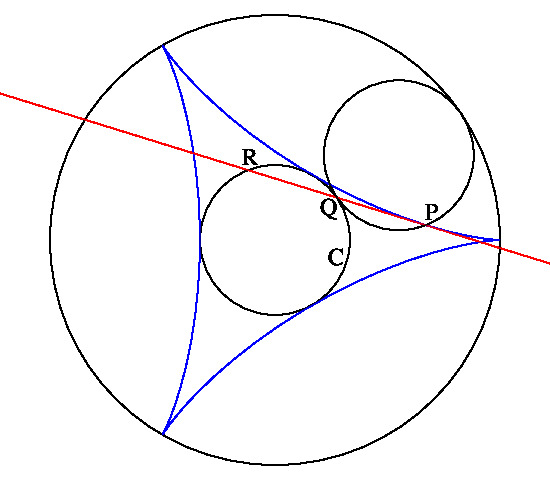　t₀ = π / 3, π, 5π / 3 のときかつそのときに限り P = Q = R となります。 即ち, C とデルトイド曲線は三点で接します。 また, 上の R の座標は (-cos 2t₀, sin 2t₀) ですから, 原点と R を結ぶ直線と x軸のなす角は π - 2t₀ (0 < t₀ < 2π / 3),　 3π - 2t₀ (2π / 3 < t₀ < 4π / 3),　 5π - 2t₀ (4π / 3 < t₀ < 2π) となります。 したがって, C 上の弧 QR を 1 : 2 に内分する点は C とデルトイド曲線の接点になります。
　0 < t₁ < π に対して S = (f(t₁), g(t₁)), T = (f(t₁ + π), g(t₁ + π)) とすれば, 線分 ST の長さは 2 であり, 直線 ST は (sin t₁)x - (cos t₁)y = sin 3t₁ で表されますが, この直線は (f(-2t₁), g(-2t₁)) での接線です。 また, 線分 ST の中点 (cos(2t₁), -sin(2t₁)) は C 上の点です。
　なお, x = 2cos t + cos2t, y = 2sin t - sin 2t は次の式を満たします。 (x²+y²)(x²+y²+18)-8x³+24xy²-27 = 0